Maximum Flow
Flow is the concept of something moving from one vertex to another in a graph, such as money (in a financial graph), data (in a computer network), or even water (in a utility network).
A graph must have weighted edges to represent flow.
The maximum flow problem is to find the maximum possible flow from a source vertex to the target vertex.
Assuming a weighted graph where every edge has a capacity under the following constraints:
-
Flow on an edge doesn’t exceed the capacity of the edge.
-
Incoming flow is equal to outgoing flow for every vertex except
sandt.
TigerGraph’s implementation of the Maximum Flow algorithm is based on a modified version of the Edmond-Karp algorithm.
Use cases
The Maximum Flow algorithm has real world applications such as airline scheduling, and in solving circulation-demand problems.
Specifications
CREATE QUERY tg_maxflow(VERTEX source, VERTEX sink, Set<STRING> v_type,
SET<STRING> e_type, SET<STRING> reverse_e_type, STRING cap_attr,
STRING cap_type, FLOAT min_flow_threshhold = 0.001, BOOL print_accum = TRUE, BOOL display_edges = TRUE, BOOL spit_to_file = FALSE, STRING file_path = "/home/tigergraph/tg_query_output.csv")Parameters
| Parameter | Description |
|---|---|
|
Source vertex where the flow starts. |
|
Target vertex where the flow is to be sent to. |
|
Vertex types to consider in the path. |
|
Edge types to traverse. |
|
Reverse edge types to traverse. |
|
Name of the attribute that contains the capacity of the edge. |
|
Data type of the |
|
Minimum flow for an edge to carry if it is to carry any flow. |
|
If true, output JSON to standard output. |
|
If true, the resulting path includes edges in addition to vertices. |
|
If true, the file output will contain every edge and how much flow they would carry to achieve the maximum flow. |
|
If not empty, write output to this file. |
Output
- JSON result
-
The return value is the maximum flow that can be carried from the source to the sink. If you set
display_edgesto true, the result will contain all edges that carry flow. However, it does not output how much flow each edge carries to achieve the maximum flow. - CSV result
-
The first line is the maximum flow that can be carried from the source to the sink. If you set
split_to_fileto true, the result will contain all edges that carry flow as well as how much flow they carry to achieve maximum flow.
Example
Suppose we have the following four areas a, b, c and d in a city.
Between each area is a pipeline that can be used to deliver water.
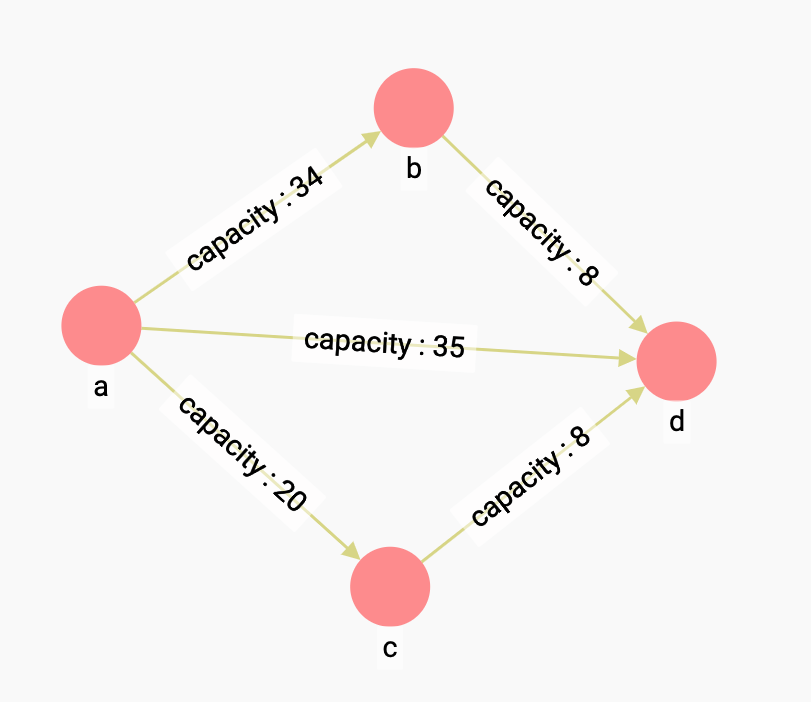
If a is the source and d is the target (the sink), the maximum flow from a to d in this network is 51.
With the edge from a to d carrying 35, and the remaining edges each carrying 8.
If we run the max flow algorithm on this network, we will get the result that the maximum flow is from a to d is 51:
RUN QUERY tg_maxflow (("a", "area"), ("d", "area"), ["area"], ["pipeline"], ["reverse_pipeline"], "capacity", "FLOAT", _, _, _, TRUE, _){
"error": false,
"message": "",
"version": {
"schema": 1,
"edition": "enterprise",
"api": "v2"
},
"results": [
{"@@sum_max_flow": 51},
{"@@edges_set": [
{
"from_type": "area",
"to_type": "area",
"directed": true,
"from_id": "b",
"to_id": "d",
"attributes": {"capacity": 8},
"e_type": "pipeline"
},
{
"from_type": "area",
"to_type": "area",
"directed": true,
"from_id": "c",
"to_id": "d",
"attributes": {"capacity": 8},
"e_type": "pipeline"
},
{
"from_type": "area",
"to_type": "area",
"directed": true,
"from_id": "a",
"to_id": "c",
"attributes": {"capacity": 20},
"e_type": "pipeline"
},
{
"from_type": "area",
"to_type": "area",
"directed": true,
"from_id": "a",
"to_id": "d",
"attributes": {"capacity": 35},
"e_type": "pipeline"
},
{
"from_type": "area",
"to_type": "area",
"directed": true,
"from_id": "a",
"to_id": "b",
"attributes": {"capacity": 34},
"e_type": "pipeline"
}
]}
]
}Maxflow: 51
From,To,Flow
a,c,8
c,d,8
a,b,8
b,d,8
a,d,35