Weakly Connected Components
In a graph, there may not always be connections between every vertex and every other vertex. In some cases, there may be components, which are defined as connected subgraphs that are not connected to other subgraphs.
A connected component is the maximal set of connected vertices inside a graph, plus their connecting edges. Inside a connected component, you can reach each vertex from each other vertex.
Graph theory distinguishes between strong and weak connections:
-
A subgraph is strongly connected if it is directed and if every vertex is reachable from every other following the edge directions.
-
A subgraph is weakly connected if it is undirected or if the only connections that exist for some vertex pairs go against the edge directions.
This Weakly Connected Components algorithm runs on graphs with undirected edges and finds connected components. It assigns a component ID to each vertex. Vertices in the same component get the same component ID.
This algorithm can be used as a helper algorithm to find existing communities and create community IDs before other algorithms are run on the graph.
Illustration
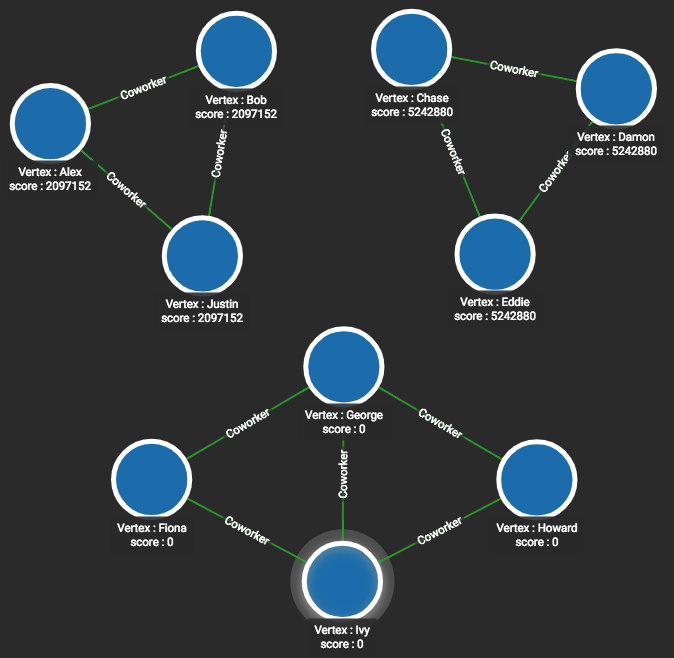
There are three components in the following figure.
The score attribute for each vertex is equivalent to the community ID.
Specifications
CREATE QUERY tg_wcc (SET<STRING> v_type, SET<STRING> e_type, INT output_limit = 100,
BOOL print_accum = TRUE, STRING result_attr = "", STRING file_path = "")Time complexity
This algorithm has a time complexity of \$O(E*d)\$, where \$E\$ is the number of edges and \$d\$ is the maximum component diameter.
Space complexity
This algorithm has a space complexity of \$O(V)\$, where \$V\$ is the number of vertices.
Output
Assigns a component ID (INT) to each vertex, such that members
of the same component have the same id value.
The return value in JSON includes all vertices and the component they belong to, as well as a map of the components with their ID and size.
Parameters
| Parameter | Description | Default |
|---|---|---|
|
Names of vertex types to use |
(empty set of strings) |
|
Names of edge types to use |
(empty set of strings) |
|
The maximum number of vertices to output in JSON format.
Use |
|
|
Whether to print the JSON to the standard output. |
False |
|
The vertex attribute where community ID values will be stored.
Must be of type |
(empty string) |
|
If not empty, write the output to this file. |
(empty string) |
Example
RUN QUERY tg_wcc(["Person"], ["Coworker"], _, _, _, _)It is easy to see in this small graph that the algorithm correctly groups the vertices:
-
Alex, Bob, and Justin all have Community ID =
2097152 -
Chase, Damon, and Eddie all have Community ID =
5242880 -
Fiona, George, Howard, and Ivy all have Community ID =
0
Our algorithm uses the TigerGraph engine’s internal vertex ID numbers. Currently there is no ability to customize the community IDs.
