PageRank
The PageRank algorithm measures the influence of each vertex on every other vertex. PageRank influence is defined recursively: a vertex’s influence is based on the influence of the vertices which refer to it. A vertex’s influence tends to increase if either of these conditions are met:
-
It has more referring vertices
-
Its referring vertices have higher influence
The analogy to social influence is clear.
A common way of interpreting PageRank value is through the Random Network Surfer model. A vertex’s PageRank score is proportional to the probability that a random network surfer will be at that vertex at any given time. A vertex with a high PageRank score is a vertex that is frequently visited, assuming that vertices are visited according to the following Random Surfer scheme:
-
Assume a person travels or surfs across a network’s structure, moving from vertex to vertex.
-
The surfer can start anywhere. This start-anywhere property is part of the magic of PageRank, meaning the score is a truly fundamental property of the graph structure itself.
-
Each round, the surfer randomly picks one of the outward connections from the surfer’s current location. The surfer repeats this random walk for a long time.
-
There is a small probability that the surfer’s next step will be a random vertex instead of a connected vertex. This probability is expressed in the algorithm as (1 - damping).
Notes
For more information, see the Google paper on PageRank.
Specifications
tg_pagerank (STRING v_type, STRING e_type, FLOAT max_change=0.001, INT max_iter=25, FLOAT damping=0.85, INT top_k = 100, BOOL print_accum = TRUE, STRING result_attr = "", STRING file_path = "", BOOL display_edges = FALSE)Parameters
| Parameter | Description | Default |
|---|---|---|
|
Names of vertex type to use |
(empty string) |
|
Names of edge type to use |
(empty string) |
|
PageRank will stop iterating when the largest difference between any vertex’s current score and its previous score ≤
|
0.001 |
|
Maximum number of iterations. |
25 |
|
Fraction of score that is due to the score of neighbors. The balance (1 - damping) is a minimum baseline score that every vertex receives. |
0.85 |
|
Sort the scores highest first and output only this many scores |
100 |
|
If True, output JSON to standard output |
True |
|
If not empty, store PageRank values in |
(empty string) |
|
If not empty, write output to this file. |
(empty string) |
|
If true, include the graph’s edges in the JSON output, so that the full graph can be displayed. |
False |
Example
# Use _ for default values
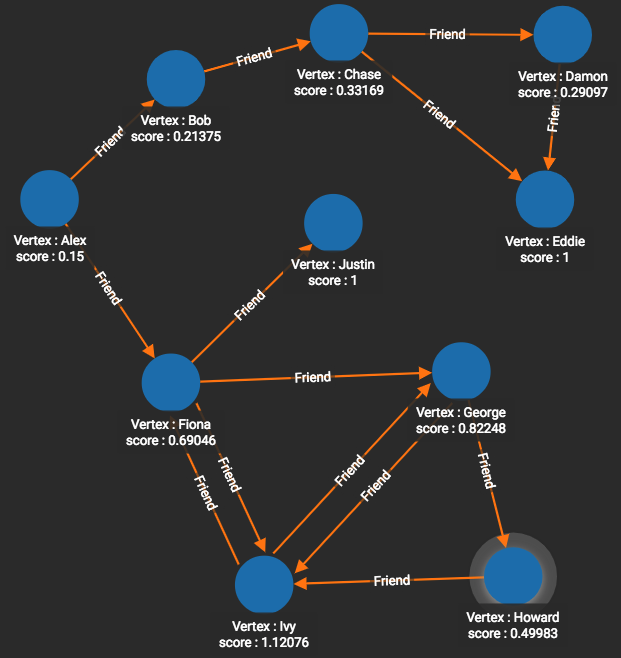
RUN QUERY tg_pagerank("Person", "Friend", 0.001, 25, 0.85, 100 _, _, _, _)We ran PageRank on our test10 graph (using Friend edges) with the following parameter values:
-
damping=0.85
-
max_change=0.001
-
max_iter=25
We see that Ivy (center bottom) has the highest PageRank score (1.12). This makes sense since there are 3 neighboring persons who point to Ivy, more than for any other person. Ivy’s high PageRank score indicates that Ivy is a relatively important person in this social group.
Eddie and Justin have scores of exactly 1 because they do not have any out-edges. This is an artifact of our particular version of PageRank. Likewise, Alex has a score of 0.15. This comes from (1 - damping), because Alex has no in-edges, meaning that Alex could only have been reached by a random visit rather than a directed connection.