ArticleRank
ArticleRank is an algorithm that has been derived from the PageRank algorithm to measure the influence of journal articles.
Page Rank assumes that relationships originating from low-degree vertices have a higher influence than relationships from high-degree vertices. Article Rank keeps the PageRank methodology but modifies the formula to lower the influence of low-degree nodes.
The Article Rank of a node \(v\) at iteration \(i\) is defined as:
Within the formula:
-
\(N_{in}(v)\) are the incoming neighbors and \(N_{out}(v)\) are the outgoing neighbors of node \(v\).
-
\(d\) is a damping factor in [0, 1], usually set to 0.85.
-
\(\overline{N_{out}}\) is the average outdegree.
Notes
For more information, see ArticleRank: a PageRank‐based alternative to numbers of citations for analysing citation networks.
Specifications
CREATE QUERY tg_article_rank (STRING v_type, STRING e_type,
FLOAT max_change=0.001, INT max_iter=25, FLOAT damping=0.85, INT top_k = 100, BOOL print_accum = TRUE, STRING result_attr = "", STRING file_path = "")Parameters
| Name | Description |
|---|---|
|
A vertex type. |
|
An edge type. |
|
Article Rank will stop iterating when the largest
difference between any vertex’s current score and its previous score ≤
|
|
Maximum number of iterations. |
|
The damping factor. Usually set to 0.85. |
|
The number of results with the highest scores to return. |
|
If true, print JSON output. |
|
If not empty, store the article rank score of each vertex in this attribute. |
|
If not empty, write output to this file. |
Example
Suppose we have the following graph:
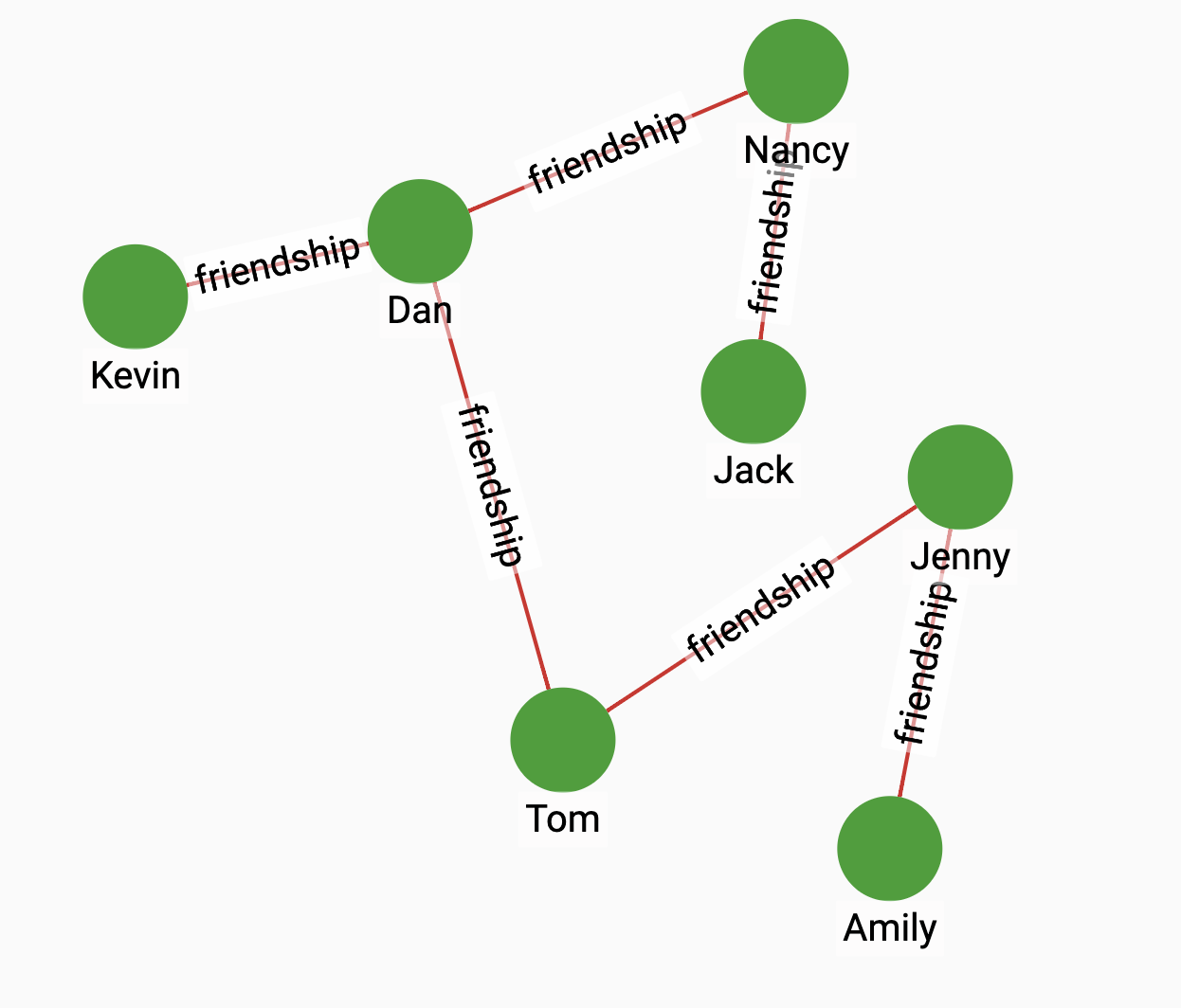
By running Article Rank on the graph, we will see that the vertex with the highest score is Dan:
RUN QUERY tg_article_rank ("person", "friendship", _, _, _, _, _){
"error": false,
"message": "",
"version": {
"schema": 2,
"edition": "enterprise",
"api": "v2"
},
"results": [{"@@topScores": [
{
"score": 2348294.75,
"Vertex_ID": "Dan"
},
{
"score": 1863160.625,
"Vertex_ID": "Jenny"
},
{
"score": 1442890.5,
"Vertex_ID": "Tom"
},
{
"score": 1053484.625,
"Vertex_ID": "Nancy"
},
{
"score": 739327.9375,
"Vertex_ID": "Kevin"
},
{
"score": 703562.75,
"Vertex_ID": "Amily"
},
{
"score": 498013.25,
"Vertex_ID": "Jack"
}
]}]
}