Harmonic Centrality
Harmonic Centrality is a variant of Closeness Centrality. In a (not necessarily connected) graph, the harmonic centrality reverses the sum and reciprocal operations in the definition of closeness centrality:
The Harmonic Centrality algorithm calculates a harmonic centrality score for each vertex in the graph.
Notes
For more information, see the paper on Harmonic Centrality: Marchiori and Latora 2000, Harmony in the Small-World.
Specifications
CREATE QUERY harmonic_cent(SET<STRING> v_type, SET<STRING> e_type,
SET<STRING> re_type,INT max_hops=10, INT top_k=100,
BOOL wf = TRUE,BOOL print_accum = True, STRING result_attr = "",
STRING file_path = "", BOOL display_edges = FALSE)Parameters
| Name | Description | Default value |
|---|---|---|
|
Vertex types to calculate harmonic centrality for |
(empty set of strings) |
|
Edge types to traverse |
(empty set of strings) |
|
Reverse edge types to traverse |
(empty set of strings) |
|
The maximum number of hops the algorithm considers for each vertex. If set to a non-positive value, the limit is ignored. |
10 |
|
Output the highest |
100 |
|
Whether to use the Wasserman-Faust normalization for multi-component graphs |
True |
|
Whether to output JSON to standard output |
True |
|
If not empty, store centrality values in FLOAT format to this attribute |
(empty string) |
|
If not empty, write output to this file in CSV. |
(empty string) |
|
Whether to include the graph’s edges in the JSON output so that the full graph can be displayed. |
False |
Output
Returns a centrality score for all vertices of the specified type in the graph. The results are ordered from most central to least central.
Result size
There is an optional parameter, top_k, that limits the results to an arbitrary number of vertices with the highest centrality scores in the graph.
This can be useful for larger graphs, since in large graphs there are likely to be many vertices with very low centrality.
The maximum result size is equal to \(V\), the number of vertices, because one centrality score is calculated for each vertex.
Example
If we have the following graph, we can see that Ivy is the most central of the five vertices. Running the algorithm on the graph shows that Ivy has the highest centrality score:
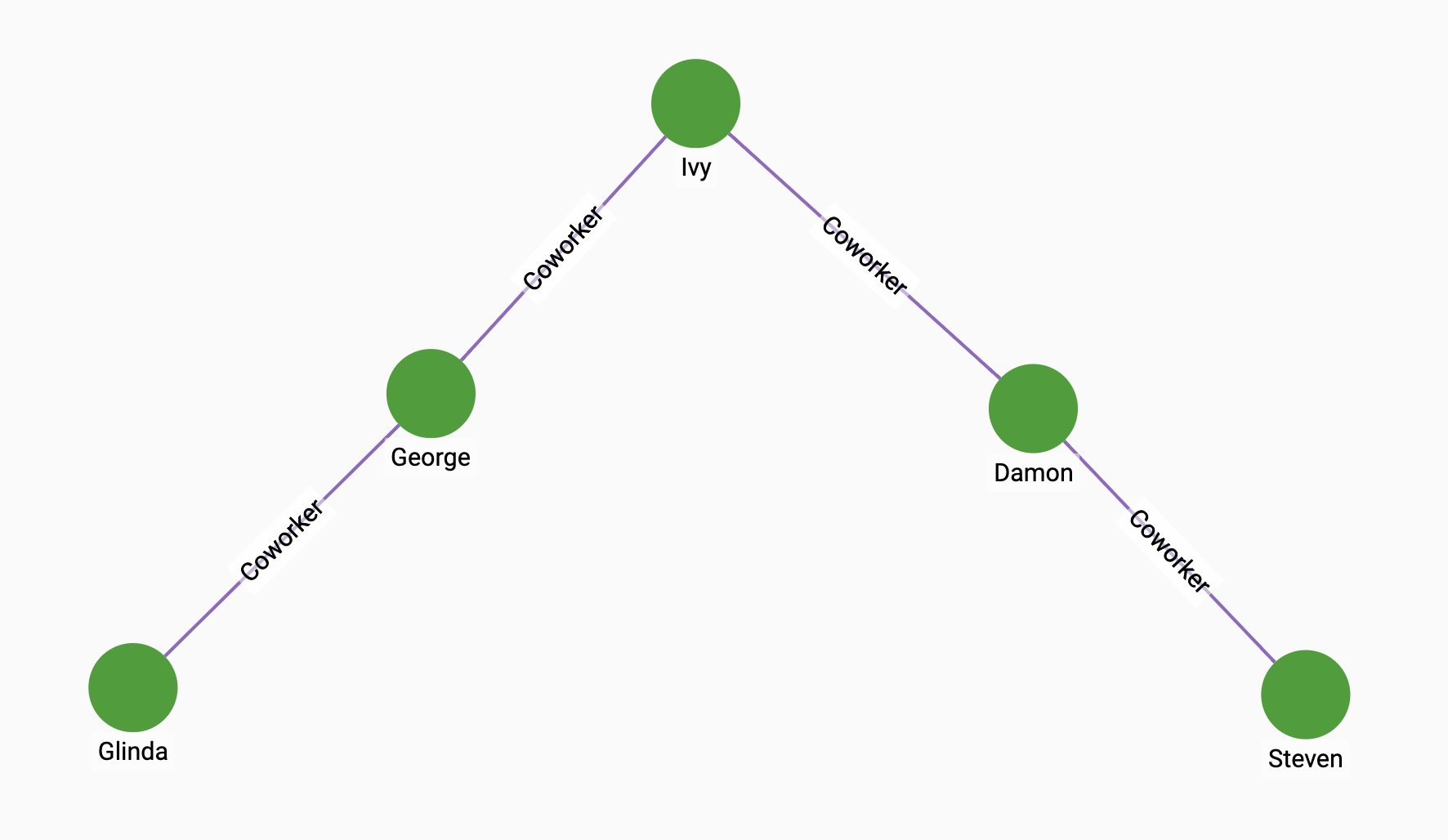
RUN QUERY harmonic_cent(["Person"], ["Coworker"], ["Coworker"], 4, 5,
true, true, _, _, _){
"error": false,
"message": "",
"version": {
"schema": 0,
"edition": "enterprise",
"api": "v2"
},
"results": [{"top_scores": [
{
"score": 0.04167,
"Vertex_ID": "Ivy"
},
{
"score": 0.03571,
"Vertex_ID": "Damon"
},
{
"score": 0.03571,
"Vertex_ID": "George"
},
{
"score": 0.025,
"Vertex_ID": "Steven"
},
{
"score": 0.025,
"Vertex_ID": "Glinda"
}
]}]
}