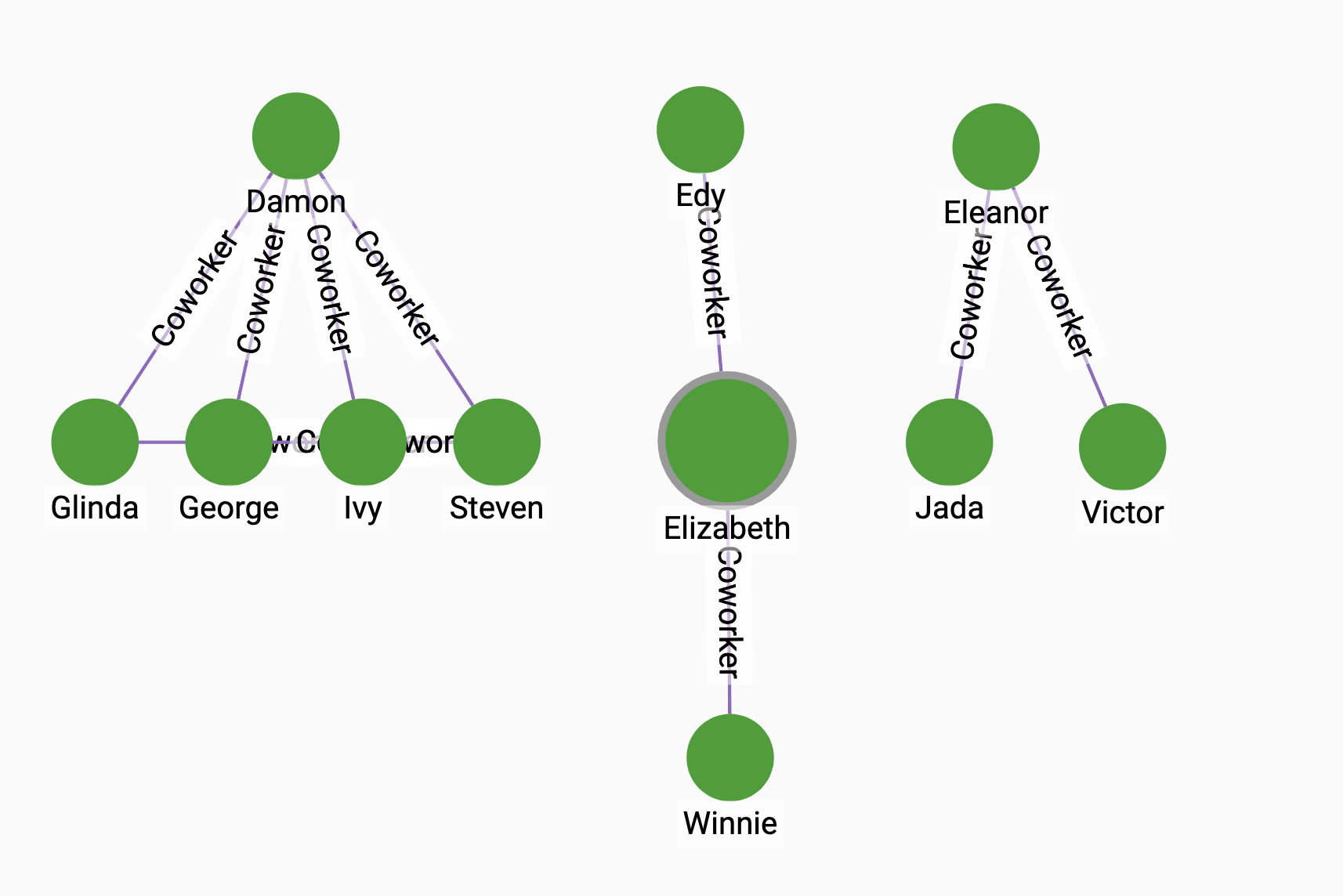
WCC (Small-World Optimized)

Supported Graph Characteristics

Unweighted edges

Homogeneous vertex types

Heterogeneous vertex types

Algorithm link: WCC (Small-World Optimized)

In addition to the regular weakly connected component algorithm, we also provide a version that is optimized for small-world graphs. A small world graph means the graph has a hub community, where the vast majority of the vertices in the graph are weakly connected.

This version improves upon the performance of the original algorithm when dealing with small-world graphs by combining several methods used to find connected components in a multi-step process.

The algorithm starts by selecting an initial pivot vertex v with a high product of indegree and outdegree. From the initial pivot vertex, the algorithm uses Breadth-First Search to determine the massive weakly connected component. The vertices that are not included in this SCC are passed off to the next step.

After identifying the first WCC, the algorithm uses the coloring method to identify the WCCs in the remaining vertices.

Notes

We use a default value of 100000 for the threshold used to choose initial pivot vertices to increase the chances that the initial pivot is contained within the largest WCC.

References

Slota et al., BFS and Coloring-based Parallel Algorithms for Strongly Connected Components and Related Problems.

Specifications

CREATE QUERY tg_wcc_small_world(STRING v_type, STRING e_type,
UINT threshold = 100000, BOOL print_results=FALSE)

Parameters

Name Description Default value

Name	Description	Default value
`STRING v_type`	The vertex type to count as part of a connected component	(empty string)
`STRING e_type`	The edge type to traverse	(empty string)
`UINT threshold`	The threshold used to choose initial pivot vertices. Only vertices whose product of indegree and outdegree exceed this threshold will be considered candidates for the pivot vertex.	`100000`
`BOOL print_results`	If true, the algorithm will return the number of vertices in each connected component.	True

STRING v_type

The vertex type to count as part of a connected component

(empty string)

STRING e_type

The edge type to traverse

(empty string)

UINT threshold

The threshold used to choose initial pivot vertices. Only vertices whose product of indegree and outdegree exceed this threshold will be considered candidates for the pivot vertex.

100000

BOOL print_results

If true, the algorithm will return the number of vertices in each connected component.

True

Output

If print_results is set to true, the algorithm will return the number of vertices in each weakly connected component.

Time complexity

The algorithm has a time complexity of \(O(E*d)\), where \(E\) is the number of edges and \(d\) is max(diameter of components).

Example

Suppose we have the following graph. We can see that there are three connected components. The first one has 5 vertices, while the two others have 3 vertices.

GSQL Command
Result

RUN QUERY tg_wcc_small_world("Person", "Coworker", _, true)

{
  "error": false,
  "message": "",
  "version": {
    "schema": 0,
    "edition": "enterprise",
    "api": "v2"
  },
  "results": [{"@@CC_count": {
    "1048576": 5,
    "1048577": 3,
    "4194306": 3
  }}]
}