Closeness Centrality

Supported Graph Characteristics

Unweighted edges

Directed edges

Undirected edges

Homogeneous vertex types

Heterogeneous vertex types

We all have an intuitive understanding when we say a home, an office, or a store is "centrally located." Something that is centrally located is roughly equidistant from several destinations.

Closeness Centrality provides a precise measure of how "centrally located" all the vertices are. The steps below show the steps for one vertex v:

Step	Mathematical Formula
1. Compute the average distance from vertex v to every other vertex:	\(d_{avg}(v) = \sum_{u \ne v} dist(v,u)/(n-1)\)
2. Invert the average distance, so we have average closeness of v:	\(CC(v) = 1/d_{avg}(v)\)

Step

Mathematical Formula

1. Compute the average distance from vertex v to every other vertex:

\(d_{avg}(v) = \sum_{u \ne v} dist(v,u)/(n-1)\)

2. Invert the average distance, so we have average closeness of v:

\(CC(v) = 1/d_{avg}(v)\)

This is repeated across all vertices in the graph.

Notes

The reverse_e_type (reverse edge type) parameter is always required. For undirected edges, use the same value for both e_type and reverse_e_type.

References

TigerGraph’s closeness centrality algorithm uses multi-source breadth-first search (MS-BFS) to traverse the graph and calculate the sum of a vertex’s distance to every other vertex in the graph, which vastly improves the performance of the algorithm.

The algorithm’s implementation of MS-BFS is based on the paper The More the Merrier: Efficient Multi-source Graph Traversal by Then et al.

Specifications

tg_closeness_cent (SET<STRING> v_type_set, SET<STRING> e_type_set, INT max_hops=10,
  INT top_k=100, BOOL wf = TRUE, BOOL print_results = True, STRING result_attribute = "",
  STRING file_path = "", BOOL display_edges = FALSE)

Parameters

Parameter Description Default

Parameter	Description	Default
`SET<STRING> v_type_set`	Vertex types to use	(empty set of strings)
`SET<STRING> e_type_set`	Edge types to use	(empty set of strings)
`SET<STRING> reverse_e_type_set`	Reverse edge types to use	(empty set of strings)
`INT max_hops`	If >=0, look only this far from each vertex	10
`INT top_k`	Output only this many scores (scores are always sorted highest to lowest)	100
`BOOL wf`	Whether to use Wasserman-Faust normalization for multi-component graphs	True
`BOOL print_results`	If True, output JSON to standard output	True
`STRING result_attribute`	If not empty, store centrality values in `FLOAT` format to this vertex attribute	(empty string)
`STRING file_path`	If not empty, write output to this file in CSV format.	(empty string)
`BOOL display_edges`	If true, include the graph’s edges in the JSON output so that the full graph can be displayed.	False

SET<STRING> v_type_set

Vertex types to use

(empty set of strings)

SET<STRING> e_type_set

Edge types to use

(empty set of strings)

SET<STRING> reverse_e_type_set

Reverse edge types to use

(empty set of strings)

INT max_hops

If >=0, look only this far from each vertex

INT top_k

Output only this many scores (scores are always sorted highest to lowest)

100

BOOL wf

Whether to use Wasserman-Faust normalization for multi-component graphs

True

BOOL print_results

If True, output JSON to standard output

True

STRING result_attribute

If not empty, store centrality values in FLOAT format to this vertex attribute

(empty string)

STRING file_path

If not empty, write output to this file in CSV format.

(empty string)

BOOL display_edges

If true, include the graph’s edges in the JSON output so that the full graph can be displayed.

False

Output

Computes a Closeness Centrality value (FLOAT type) for each vertex, calculated from the average distance between that vertex and every other vertex.

Result size

\(V\), or the number of vertices. One FLOAT value is returned for each vertex.

Time complexity

This algorithm has a time complexity of \(O(E*V)\) where \(E\) is the number of edges and \(V\) is the number of vertices.

Parallel processing reduces the time needed for computation.

Run commands

Schema-Free Query

RUN QUERY tg_closeness_cent (<parameters>)

Packaged Template Query

CALL GDBMS_ALGO.centrality.closeness_cent (<parameters>)

Example

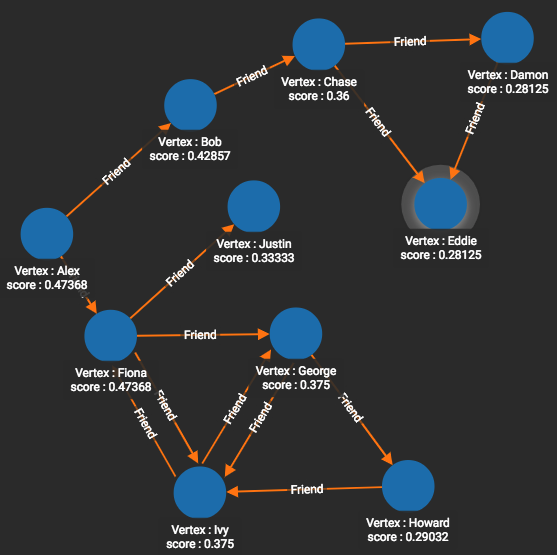
Closeness centrality can be measured for either directed edges (from v to others) or for undirected edges. Directed graphs may seem less intuitive, however, because if the distance from Alex to Bob is 1, it does not mean the distance from Bob to Alex is also 1.

For our example, we wanted to use the topology of a friendship graph, but to have undirected edges. We emulated an undirected graph by using both Friend and Also_Friend (reverse-direction) edges.

# Use _ for default values
RUN QUERY tg_closeness_cent(["Person"], ["Friend", "Also_Friend"], _, _,
_, _, _, _, _)

Visualized results of example query on social10 graph