Louvain

Supported Graph Characteristics

Weighted edges

Undirected edges

Homogeneous vertex types

Heterogeneous vertex types

Algorithm link: Louvain

The Louvain Method for community detection ^[1] partitions the vertices in a graph by approximately maximizing the graph’s modularity score.

A graph with high modularity has its vertices partitioned into communities, or modules, such that connections inside the communities are dense and connections to other communities are sparse. The task is to find the optimal way to partition the vertices.

Figure 1. A graph showing three distinct modules, each with dense connections inside and few connections to other modules.

One of the most efficient and empirically effective methods for calculating modularity was published by a team of researchers at the University of Louvain in Belgium. The Louvain method uses agglomeration and hierarchical optimization:

Optimize modularity for small local communities.
Treat each optimized local group as one unit, and repeat the modularity operation for groups of these condensed units.

To create the starting conditions, the algorithm assigns an initial community label to every vertex and calculates the base modularity score for the graph.

Next, the algorithm calculates the modularity score change of moving every vertex into every other community. Once a score is calculated for every possible change, the algorithm moves each vertex to the community that results in the highest modularity score change.

The community labels are changed repeatedly until the modularity score no longer increases.

The next phase "coarsens" the graph by aggregating the vertices in the same community into one vertex.

The algorithm repeats these steps to move vertices into new communities and coarsen the graph to reduce the total number of vertices until either of these conditions is met:

The graph modularity score no longer increases with any vertex reassignment into any new community
The number of iterations of the reassignment-coarsen-measure cycle meets a pre-defined limit (the default is 10 iterations)

The process of checking the modularity score increase for every possible vertex and community assignment is slow for large graphs.

Notes

Louvain only works with directed graphs if reverse edges are included.

An improved Parallel Louvain Method (PLM) calculates the best community to move to for each vertex in parallel^[2]. In the Parallel Louvain Method (PLM), the positive modularity gain is not guaranteed, which may result in swapping two vertices to each other’s community.

Specifications

CREATE QUERY tg_louvain( SET<STRING> v_type_set,  SET<STRING> e_type_set,
    STRING weight_attribute = "weight", INT maximum_iteration = 10,
    STRING result_attribute = "cid", STRING file_path = "",
    BOOL print_info = FALSE)

Parameters

Parameter Description Default

Parameter	Description	Default
`SET<STRING> v_type_set`	Names of vertex types to use	(empty string)
`SET<STRING> e_type_set`	Names of edge types to use	(empty string)
`STRING weight_attribute`	Name of edge weight attribute (the specified attribute must be of type `FLOAT`)	(empty string)
`INT maximum_iteration`	Maximum number of iterations	10
`STRING result_attribute`	If not empty, store community values in `INT` format to this vertex attribute	(empty string)
`STRING file_path`	If not empty, write output to this file.	(empty string)
`BOOL print_info`	If true, print results to JSON output.	`True`

SET<STRING> v_type_set

Names of vertex types to use

(empty string)

SET<STRING> e_type_set

Names of edge types to use

(empty string)

STRING weight_attribute

Name of edge weight attribute (the specified attribute must be of type FLOAT)

(empty string)

INT maximum_iteration

Maximum number of iterations

STRING result_attribute

If not empty, store community values in INT format to this vertex attribute

(empty string)

STRING file_path

If not empty, write output to this file.

(empty string)

BOOL print_info

If true, print results to JSON output.

True

Output

If result_attribute is provided, the algorithm assigns a module ID (INT) to each vertex, such that members of the same module have the same ID value.

if print_info is set to true or file_path is provided, the JSON or .csv output contains the following information:

The number of vertices and communities in the graph.
The heuristic statistics used by Louvain.

Time complexity

This algorithm has a time complexity of \(O(V^2*L)\), where \(V\) is the number of vertices and \(L\) is the total number of iterations.

Example

You can run the algorithm on the social10 graph by slightly modifying the schema. Since the algorithm requires weighted edges, we can add an attribute to all edges and set edge weight to 1.

By running the algorithm on social10, we can see that the vertices that are in the same community have more intra-community edges than inter-community edges.

Run command
Visualized result
JSON result

RUN QUERY tg_louvain(["Person"], ["Coworker","Friend"], "weight", _, _, _, TRUE)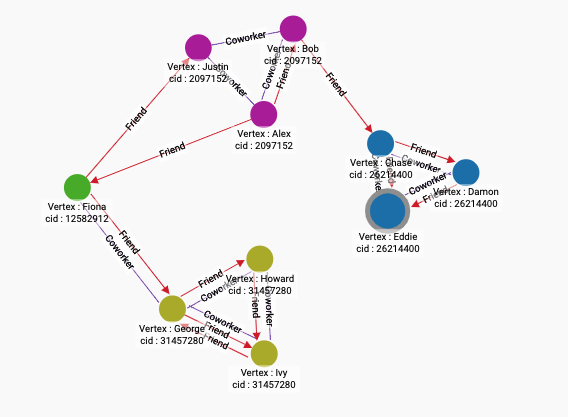

{
  "error": false,
  "message": "",
  "version": {
    "schema": 1,
    "edition": "enterprise",
    "api": "v2"
  },
  "results": [
    {"AllVertexCount": 10},
    {"InitChangeCount": 7},
    {"IterChangeCount": 0},
    {"VertexFollowedToCommunity": 0}, (1)
    {"VertexFollowedToVertex": 0}, (2)
    {"VertexAssignedToItself": 0},
    {"FinalCommunityCount": 4}
  ]
}

1	Number of vertices followed to community assigned by Louvain.
2	Number of vertices followed to their only neighbors. For example, if we have (A)---(B), A and B will become a community with only vertex A and B.

1. Blondel, Vincent D., et al. "Fast unfolding of communities in large networks." Journal of statistical mechanics: theory and experiment 2008.10 (2008): P10008.

2. Staudt, Christian L., and Henning Meyerhenke. "Engineering parallel algorithms for community detection in massive networks." IEEE Transactions on Parallel and Distributed Systems 27.1 (2016): 171-184.