Strongly Connected Components
A strongly connected component (SCC) is a subgraph such that there is a path from any vertex to every other vertex. A graph can contain more than one separate SCC. This SCC algorithm finds the maximal SCCs within a graph.
Our implementation is based on the Divide-and-Conquer Strong Components (DCSC) algorithm:
-
In each iteration, pick a pivot vertex
vrandomly. -
Find its descendant and predecessor sets:
-
Descendant set
D_vis the set of vertices reachable fromvusing regular edges. -
Predecessor set
P_vis the set of vertices reachable fromvusing reverse edges.
-
-
The intersection of these two sets is a strongly connected component
SCC_v.
The graph can be partitioned into 4 sets:
-
SCC_v -
Descendants
D_vexcludingSCC_v -
Predecessors
P_vexcludingSCC_v -
Remainders
R_v.
It is proved that any SCC is a subset of one of the 4 sets.
Thus, we can divide the graph into different subsets and detect the SCCs independently and iteratively.
Notes
The implementation of this algorithm requires reverse edges for all directed edges considered in the graph.
The problem of this algorithm is unbalanced load and slow convergence when there are a lot of small SCCs, which is often the case in real-world use cases.
We added two trimming stages to improve the performance: Size-1 SCC Trimming and Weakly Connected Components.
References
DCSC Algorithm: Fleischer, Lisa K., Bruce Hendrickson, and Ali Pınar. "On identifying strongly connected components in parallel." International Parallel and Distributed Processing Symposium. Springer, Berlin, Heidelberg, 2000.
Size-1 SCC Trimming: Mclendon III, William, et al. "Finding strongly connected components in distributed graphs." Journal of Parallel and Distributed Computing 65.8 (2005): 901-910.
Weakly Connected Components: Hong, Sungpack, Nicole C. Rodia, and Kunle Olukotun. "On fast parallel detection of strongly connected components (SCC) in small-world graphs." Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis. ACM, 2013.
Specifications
tg_scc ( SET<STRING> v_type_set, SET<STRING> e_type_set, SET<STRING> rev_e_type,
INT top_k_dist, INT print_limit, INT maximum_iteration = 500, INT iter_wcc = 5,
BOOL print_results = TRUE, STRING result_attribute= "", STRING file_path="")Parameters
| Parameter | Description | Default Value |
|---|---|---|
|
The vertex types to use |
(empty set of strings) |
|
The edge types to use |
(empty set of strings) |
|
The reverse edge types to use |
(empty set of strings) |
|
The top k results in the SCC distribution |
N/A |
|
The maximum number of vertices to output in JSON format. |
N/A |
|
The maximum number of iterations of the algorithm. |
500 |
|
Find weakly connected components for the active vertices in this iteration, since the largest SCCs are already found after several iterations. Usually a small number (3 to 10). |
5 |
|
If true, print output in JSON format to the standard output. |
True |
|
If not empty, store community values in |
(empty string) |
|
If not empty, write output to this file. |
(empty string) |
Example
Consider a graph with Person vertices and Friend and Coworker edges. The following illustration shows a group of these vertices and edges. Not shown are a number of other vertices that have no connection to other vertices.
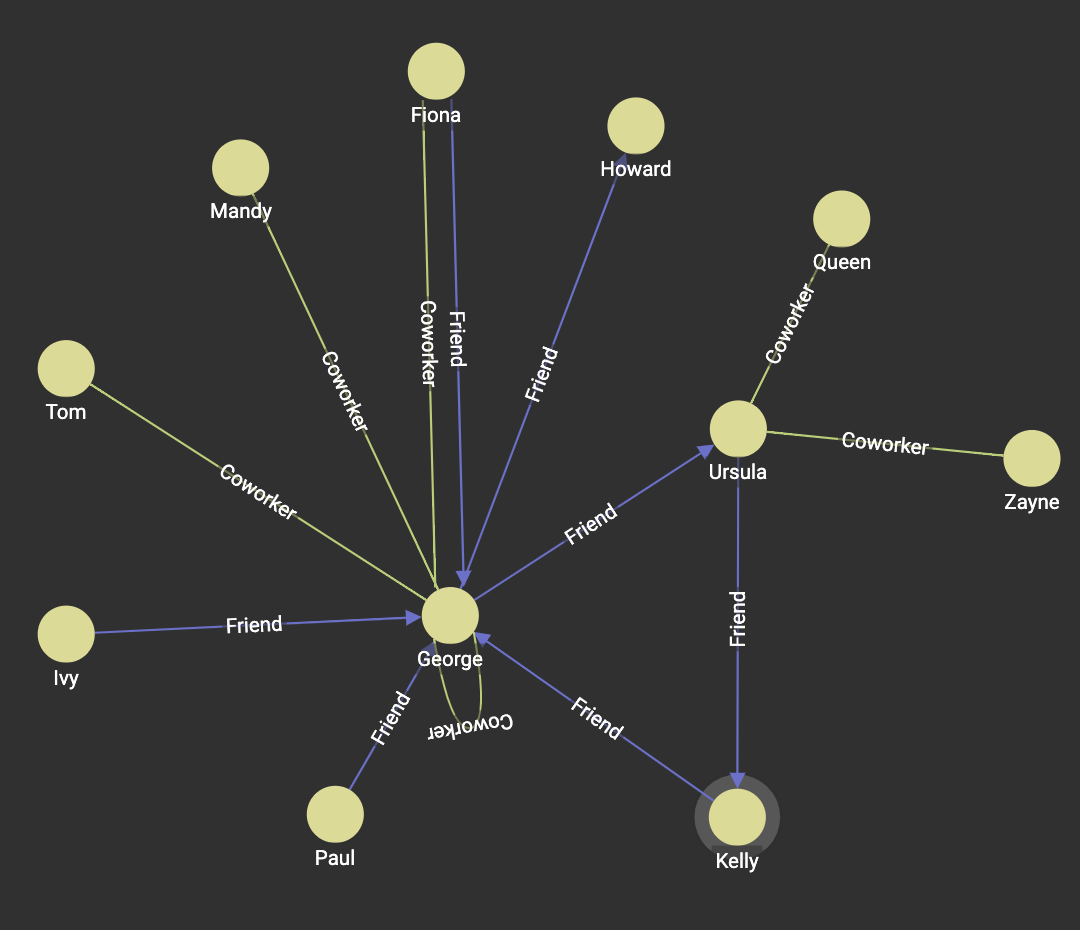
We run the SCC query with default values, making sure to include both types of edges in the query.
A portion of the JSON result is shown below.
[
{
"@@cluster_dist_heap": [
{
"csize": 9,
"num": 1
},
{
"csize": 1,
"num": 17
}
]
}
]The @@.cluster_dist_heap object reports on the size distribution of SCCs.
There is one SCC with 9 vertices, and 17 SCCs with only 1 vertex in the graph.