Betweenness Centrality

Supported Graph Characteristics

Unweighted edges

Directed edges

Undirected edges

Homogeneous vertex types

Heterogeneous vertex types

The Betweenness Centrality of a vertex is defined as the number of shortest paths that pass through this vertex, divided by the total number of shortest paths. That is

\[BC(v) =\sum_{s \ne v \ne t}PD_{st}(v)= \sum_{s \ne v \ne t} SP_{st}(v)/SP_{st}\]

where \(PD\) is the pair dependency, \(SP_{st}\)is the total number of shortest paths from node s to node t and \(SP_{st}(v)\)is the number of those paths that pass through v.

The TigerGraph implementation is based on A Faster Algorithm for Betweenness Centrality by Ulrik Brandes, Journal of Mathematical Sociology 25(2):163-177, (2001). For every vertex s in the graph, the pair dependency starting from vertex s to all other vertices t via all other vertices v is computed first:

\[PD_{s*}(v) = \sum_{t:s \in V} PD_{st}(v)\]

Then betweenness centrality is computed as

\[BC(v) =\sum_{s:s \in V}PD_{s*}(v)/2\]

According to Brandes, the accumulated pair dependency can be calculated as

\[PD_{s*}(v) =\sum_{w:v \in P_s(w)} SP_{sv}(v)/SP_{sw} \cdot (1+PD_{s*}(w)) ,\]

where \(P_s(w)\), the set of predecessors of vertex w on shortest paths from s, is defined as

\[P_s(w) = \{u \in V: \{u, w\} \in E, dist(s,w) = dist(s,u)+dist(u,w) \} .\]

For every vertex, the algorithm works in two phases. The first phase calculates the number of shortest paths passing through each vertex. Then starting from the vertex on the most outside layer in a non-incremental order with pair dependency initial value of 0, traverse back to the starting vertex.

Notes

The reverse_edge_type parameter is mandatory. If you are using undirected edges, then enter the same value for reserve_edge_type that you use for edge_type_set.

Specifications

CREATE QUERY tg_betweenness_cent(SET<STRING> v_type_set, SET<STRING> e_type_set,
STRING reverse_e_type,INT max_hops=10, INT top_k=100, BOOL print_results = True,
STRING result_attribute = "", STRING file_path = "", BOOL display_edges = FALSE)

Parameters

Parameter Description Default Value

Parameter	Description	Default Value
`SET<STRING> v_type_set`	The vertex types to use	(empty set of strings)
`SET<STRING> e_type_set`	The edge types to use	(empty set of strings)
`SET<STRING> reverse_e_type_set`	The reverse edge types to use. For undirected edges, use the same value for `e_type_set`	(empty set of strings)
`INT max_hops`	If >=0, look only this far from each vertex	10
`INT top_k`	The number of scores to output, sorted in descending order	100
`BOOL print_results`	If true, print output in JSON format to the standard output.	True
`STRING result_attribute`	If not empty, store centrality values in `FLOAT` format to this attribute	(empty string)
`STRING file_path`	If not empty, write output to this file.	(empty string)
`BOOL display_edges`	If true, include the graph’s edges in the JSON output, so that the full graph can be displayed.	True

SET<STRING> v_type_set

The vertex types to use

(empty set of strings)

SET<STRING> e_type_set

The edge types to use

(empty set of strings)

SET<STRING> reverse_e_type_set

The reverse edge types to use. For undirected edges, use the same value for e_type_set

(empty set of strings)

INT max_hops

If >=0, look only this far from each vertex

INT top_k

The number of scores to output, sorted in descending order

100

BOOL print_results

If true, print output in JSON format to the standard output.

True

STRING result_attribute

If not empty, store centrality values in FLOAT format to this attribute

(empty string)

STRING file_path

If not empty, write output to this file.

(empty string)

BOOL display_edges

If true, include the graph’s edges in the JSON output, so that the full graph can be displayed.

True

Output

Computes a Betweenness Centrality value (FLOAT type) for each vertex. The result size is equal to \(V\), the number of vertices.

Time complexity

This algorithm has a time complexity of \(O(E*V)\) where \(E\) is the number of edges and \(V\) is the number of vertices.

Considering the high time cost of running this algorithm on a big graph, users can set a maximum number of iterations. Parallel processing reduces the time needed for computation.

Run commands

Schema-Free Query

RUN QUERY tg_betweenness_cent (<parameters>)

Packaged Template Query

CALL GDBMS_ALGO.centrality.betweenness_cent (<parameters>)

Example

In this example, Claire is in the very center of the graph and has the highest betweenness centrality. Six shortest paths pass through Sam (i.e. paths from Victor to all other 6 people except for Sam and Victor), so the score of Sam is 6. David also has a score of 6, since Brian has 6 paths to other people that pass through David.

# Use _ for default values
RUN QUERY tg_betweenness_cent(["Person"], ["Friend"], _, _, _, _, _, _)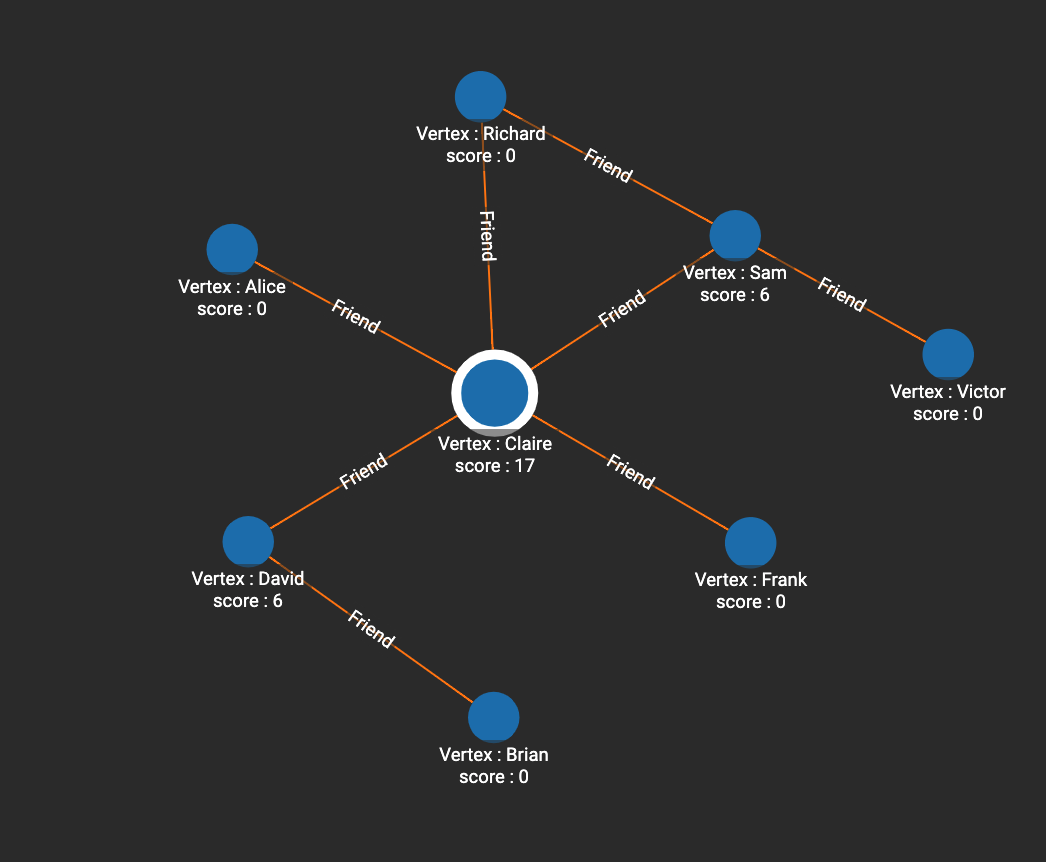

Visualized results of example query on a social graph with undirected edges Friend

[
  {
    "@@BC": {
      "Alice": 0,
      "Frank": 0,
      "Claire": 17,
      "Sam": 6,
      "Brian": 0,
      "David": 6,
      "Richard": 0,
      "Victor": 0
    }
  }
]

In the following example, both Charles and David have 9 shortest paths passing through them. Ellen is in a similar position as Charles, but her centrality is weakened due to the path between Frank and Jack.

[
  {
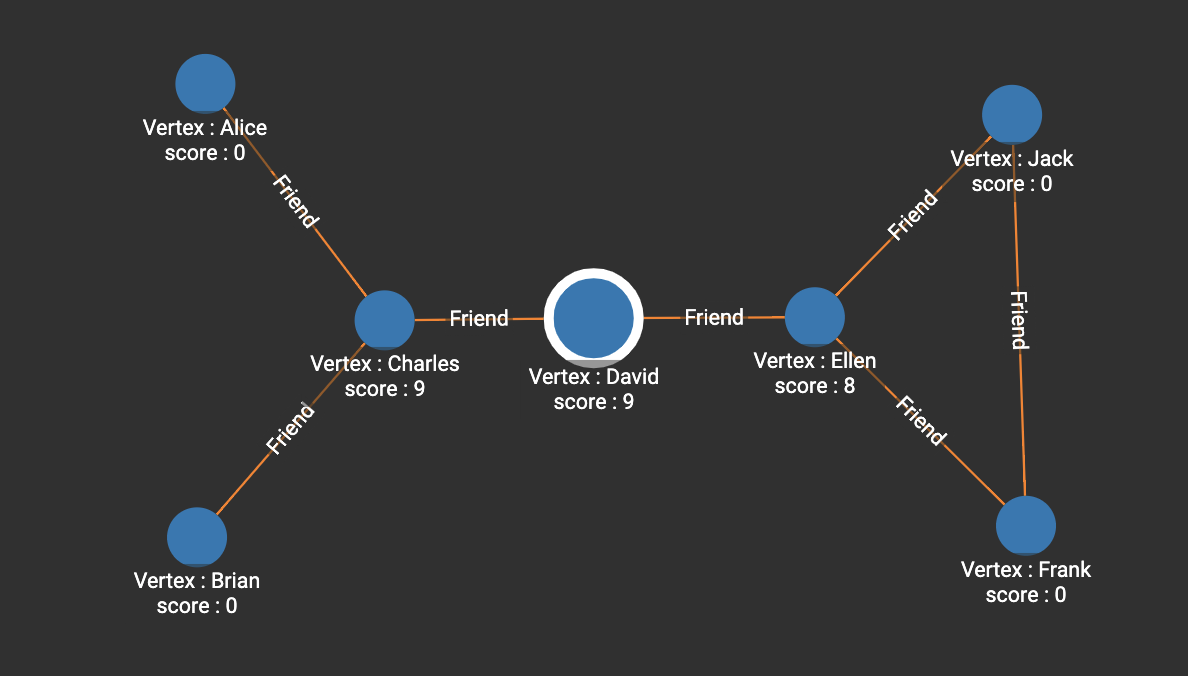
    "@@BC": {
      "Alice": 0,
      "Frank": 0,
      "Charles": 9,
      "Ellen": 8,
      "Brian": 0,
      "David": 9,
      "Jack": 0
    }
  }
]