Label Propagation
Label Propagation is a heuristic method for determining communities. The idea is simple: If the plurality of your neighbors all bear the label X, then you should label yourself as also a member of X. In effect, this propagates a label from a single vertex to a group of vertices.
The algorithm begins with each vertex having its own unique label. It then iteratively updates labels based on the neighbor influence described above. It is important that the order for updating the vertices be random.
This algorithm is favored for its efficiency and simplicity, but it is not guaranteed to produce the same results every time.
In a variant version, some vertices could initially be known to belong to the same community. If they are well-connected to one another, they are likely to preserve their common membership and influence their neighbors,
Specifications
tg_label_prop ( SET<STRING> v_type_set, SET<STRING> e_type_set, INT maximum_iteration, INT print_limit,
BOOL print_results = TRUE, STRING file_path = "", STRING attr = "")Time complexity
This algorithm has a complexity of \$O(E*k)\$, where \$E\$ is the number of edges and \$k\$ is the number of iterations.
| Parameter | Description | Default |
|---|---|---|
|
Names of vertex types to use |
(empty set of strings) |
|
Names of edge types to use |
(empty set of strings) |
|
Maximum iterations of the algorithm |
N/A |
|
Maximum number of vertices to output in JSON format |
N/A. Use |
|
Whether to print data in JSON format to the standard output |
False |
|
The file path where the output will be written to, if applicable |
(empty string) |
|
Vertex attribute where community ID values are assigned in |
(empty string) |
Example
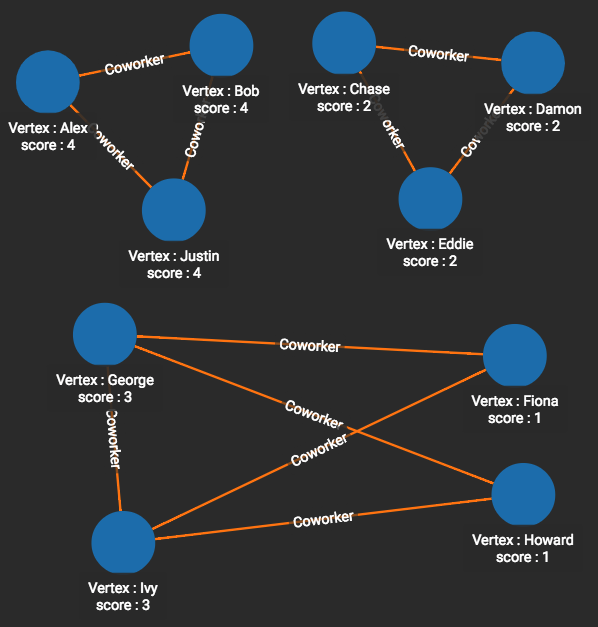
This is the same graph that was used in the Connected Component example. The results are different, though. The quartet of Fiona, George, Howard, and Ivy have been split into 2 groups:
-
(George & Ivy) each connect to (Fiona & Howard) and to one another.
-
(Fiona & Howard) each connect to (George & Ivy) but not to one another.
Label Propagation tries to find natural clusters and separations within connected components. That is, it looks at the quality and pattern of connections. The Connected Component algorithm simply asks the Yes or No question: Are these two vertices connected?
We set maximum_iteration to 10, but the algorithm reaches a steady state after 3 iterations:
# Use _ for default/empty values
RUN QUERY tg_label_prop(["Person"], ["Coworker"], 10, -1, _, _, _)