k-Nearest Neighbors
The k-Nearest Neighbors (kNN) algorithm is one of the simplest classification algorithms. It assumes that some or all the vertices in the graph have already been classified. The classification is stored as an attribute called the label. The goal is to predict the label of a given vertex, by seeing what are the labels of the nearest vertices.
Given a source vertex in the dataset and a positive integer k, the algorithm calculates the distance between this vertex and all other vertices and selects the k vertices that are nearest. The prediction of the label of this node is the majority label among its k-nearest neighbors.
The distance can be physical distance as well as the reciprocal of similarity score, in which case "nearest" means "most similar". In our algorithm, the distance is the reciprocal of cosine neighbor similarity.
The similarity calculation used here is the same as the calculation in Cosine Similarity of Neighborhoods (Single-Source). Note that in this algorithm, vertices with zero similarity to the source node are not considered in prediction. For example, if there are 5 vertices with non-zero similarity to the source vertex, and 5 vertices with zero similarity, when we pick the top 7 neighbors, only the label of the 5 vertices with non-zero similarity score will be used in prediction.
Notes
The algorithm will not output more than \$k\$ vertex pairs, so the algorithm may arbitrarily choose to output one vertex pair over another if there are tied similarity scores.
Specifications
tg_knn_cosine_ss (VERTEX source, SET<STRING> v_type_set, SET<STRING> e_type_set, SET<STRING>
reverse_e_type, STRING weight_attribute, STRING label, INT top_k,
BOOL print_results = TRUE, STRING file_path = "", STRING attr = "")
RETURNS (STRING)Parameters
| Parameter | Description | Default Value |
|---|---|---|
|
The vertex that you want to predict the labels from. Provide the vertex ID and type as a tuple: |
N/A |
|
The vertex types to use |
(empty set of strings) |
|
The edge types to use |
(empty set of strings) |
|
The reverse edge types to use |
(empty set of strings) |
|
If not empty, use this edge attribute as the edge weight. |
(empty string) |
|
If not empty, read an existing label from this attribute. |
(empty string) |
|
The number of nearest neighbors to consider |
N/A |
|
If true, print output in JSON format to the standard output. |
True |
|
If not empty, write output to this file. |
(empty string) |
|
If not empty, store the predicted label to this vertex attribute. |
(empty string) |
Example
For the movie graph, we add the following labels to the Person vertices.
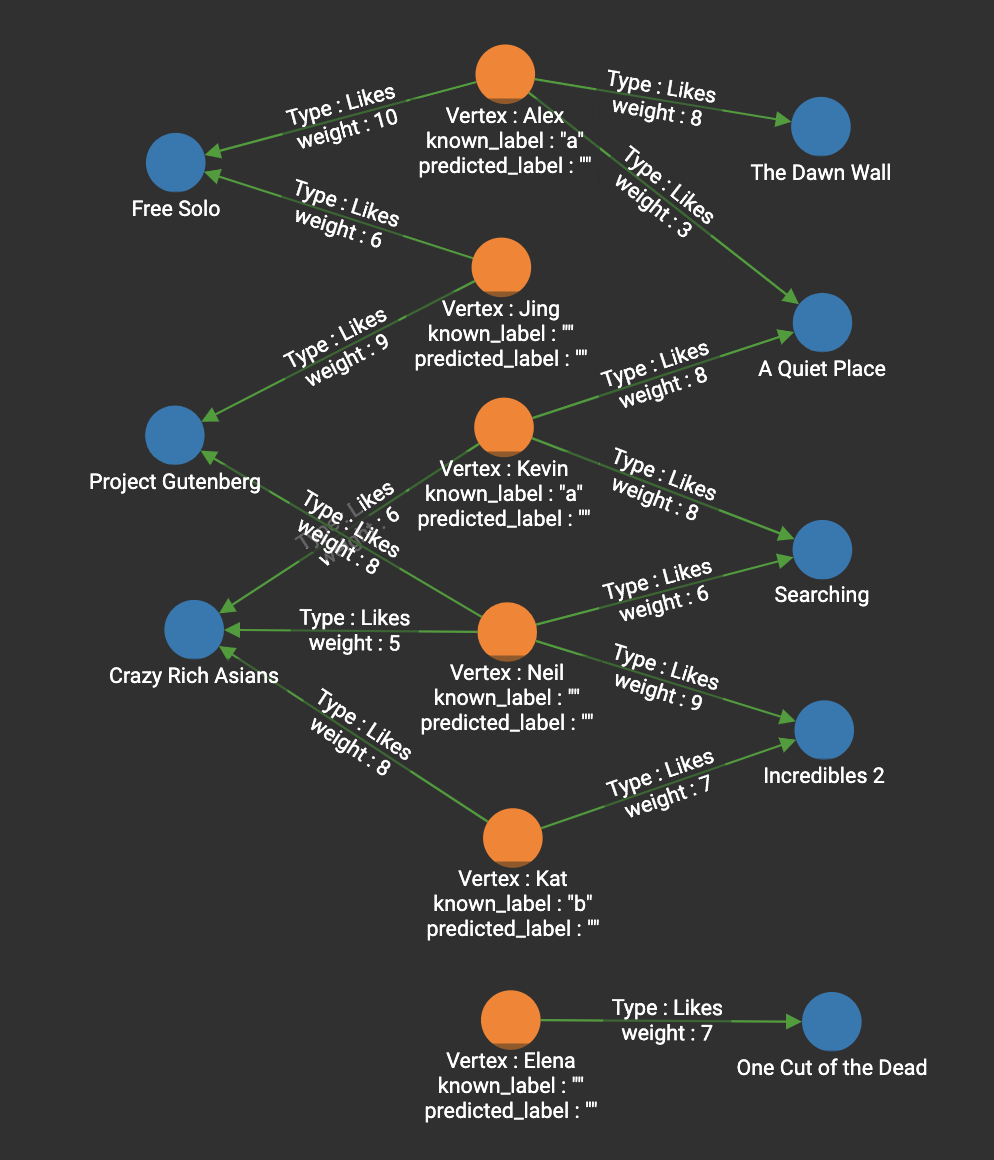
When we install the algorithm, answer the questions like:
Vertex types: Person
Edge types: Likes
Second Hop Edge type: Reverse_Likes
Edge attribute that stores FLOAT weight, leave blank if no such attribute:weight
Vertex attribute that stores STRING label:known_labelWe then run kNN, using Neil as the source person and k=3. This is the JSON output :
[
{
"predicted_label": "a"
}
]If we run cosine_nbor_ss, using Neil as the source person and k=3, we can see the persons with the top 3 similarity score:
[
{
"neighbours": [
{
"v_id": "Kat",
"v_type": "Person",
"attributes": {
"neighbours.@similarity": 0.67509
}
},
{
"v_id": "Jing",
"v_type": "Person",
"attributes": {
"neighbours.@similarity": 0.46377
}
},
{
"v_id": "Kevin",
"v_type": "Person",
"attributes": {
"neighbours.@similarity": 0.42436
}
}
]
}
]Kat has a label "b", Kevin has a label "a", and Jing does not have a label. Since "a" and "b" are tied, the prediction for Neil is just one of the labels.
If Jing had label "b", then there would be 2 "b"s, so "b" would be the prediction.
If Jing had label "a", then there would be 2 "a"s, so "a" would be the prediction.