Louvain
The Louvain Method for community detection [1] partitions the vertices in a graph by approximately maximizing the graph’s modularity score.
A graph with high modularity has its vertices partitioned into communities, or modules, such that connections inside the communities are dense and connections to other communities are sparse. The task is to find the optimal way to partition the vertices.
One of the most efficient and empirically effective methods for calculating modularity was published by a team of researchers at the University of Louvain in Belgium. The Louvain method uses agglomeration and hierarchical optimization:
-
Optimize modularity for small local communities.
-
Treat each optimized local group as one unit, and repeat the modularity operation for groups of these condensed units.
To create the starting conditions, the algorithm assigns an initial community label to every vertex and calculates the base modularity score for the graph.
Next, the algorithm calculates the modularity score change of moving every vertex into every other community. Once a score is calculated for every possible change, the algorithm moves each vertex to the community that results in the highest modularity score change.
The community labels are changed repeatedly until the modularity score no longer increases.
The next phase "coarsens" the graph by aggregating the vertices in the same community into one vertex.
The algorithm repeats these steps to move vertices into new communities and coarsen the graph to reduce the total number of vertices until either of these conditions is met:
-
The graph modularity score no longer increases with any vertex reassignment into any new community
-
The number of iterations of the reassignment-coarsen-measure cycle meets a pre-defined limit (the default is 10 iterations)
The process of checking the modularity score increase for every possible vertex and community assignment is slow for large graphs.
Notes
Louvain only works with directed graphs if reverse edges are included.
An improved Parallel Louvain Method (PLM) calculates the best community to move to for each vertex in parallel[2]. In the Parallel Louvain Method (PLM), the positive modularity gain is not guaranteed, which may result in swapping two vertices to each other’s community.
Specifications
CREATE QUERY tg_louvain( SET<STRING> v_type_set, SET<STRING> e_type_set,
STRING weight_attribute = "weight", INT maximum_iteration = 10,
STRING result_attribute = "cid", STRING file_path = "",
BOOL print_info = FALSE)Parameters
| Parameter | Description | Default |
|---|---|---|
|
Names of vertex types to use |
(empty string) |
|
Names of edge types to use |
(empty string) |
|
Name of edge weight attribute (the specified attribute must be of type |
(empty string) |
|
Maximum number of iterations |
10 |
|
If not empty, store community values in |
(empty string) |
|
If not empty, write output to this file. |
(empty string) |
|
If true, print results to JSON output. |
|
Output
If result_attribute is provided, the algorithm assigns a module ID (INT) to each vertex, such that members of the same module have the same ID value.
if print_info is set to true or file_path is provided, the JSON or .csv output contains the following information:
-
The number of vertices and communities in the graph.
-
The heuristic statistics used by Louvain.
Example
You can run the algorithm on the social10 graph by slightly modifying the schema.
Since the algorithm requires weighted edges, we can add an attribute to all edges and set edge weight to 1.
By running the algorithm on social10, we can see that the vertices that are in the same community have more intra-community edges than inter-community edges.
RUN QUERY tg_louvain(["Person"], ["Coworker","Friend"], "weight", _, _, _, TRUE)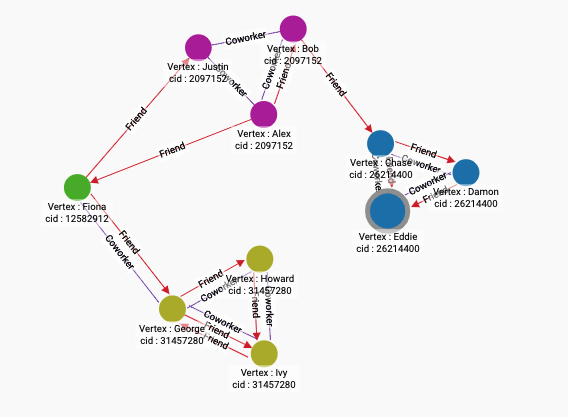
{
"error": false,
"message": "",
"version": {
"schema": 1,
"edition": "enterprise",
"api": "v2"
},
"results": [
{"AllVertexCount": 10},
{"InitChangeCount": 7},
{"IterChangeCount": 0},
{"VertexFollowedToCommunity": 0}, (1)
{"VertexFollowedToVertex": 0}, (2)
{"VertexAssignedToItself": 0},
{"FinalCommunityCount": 4}
]
}| 1 | Number of vertices followed to community assigned by Louvain. |
| 2 | Number of vertices followed to their only neighbors. For example, if we have (A)---(B), A and B will become a community with only vertex A and B. |