k-Core Decomposition

Supported Graph Characteristics

Unweighted edges

Directed edges

Undirected edges

Homogeneous vertex types

Algorithm link: k-Core Decomposition

A k-core of a graph is a maximal connected subgraph in which every vertex is connected to at least \$k\$ vertices in the subgraph.

This algorithm takes a range of values for \$k\$ and returns the vertex set that constitutes the k-core with the highest possible value of \$k\$ within the range.

To obtain the k-core of a graph, the algorithm first deletes the vertices whose outdegree is less than k. It then updates the outdegree of the neighbors of the deleted vertices, and if that causes a vertex’s outdegree to fall below k, it will also delete that vertex. The algorithm repeats this operation until every vertex left in the subgraph has an outdegree of at least k.

Notes

This is an implementation of Algorithm 2 in Scalable K-Core Decomposition for Static Graphs Using a Dynamic Graph Data Structure, Tripathy et al., IEEE Big Data 2018.

Specifications

tg_kcore(STRING v_type, STRING e_type, INT k_min = 0,
  INT k_max = -1, BOOL print_results = TRUE,
  STRING result_attribute = "", STRING file_path = "",
  BOOL print_all_k = FALSE, BOOL show_shells=FALSE)

Parameters

Parameter Description

STRING v_type

Vertex type to include in the k-core

STRING e_type

Edge type to count for k-core connections

INT k_min

Minimum value of k. If the actual maximum core is below k_min, the algorithm will return an empty set.

INT k_max

Maximum value of k. If k_max is smaller than k_min, the algorithm will ignore this parameter and keep looking for k-cores until it reaches a value of k where a k-core cannot be found.

BOOL print_results

Boolean value that decides whether the algorithm will return output in JSON

STRING result_attribute

An attribute of the vertex to save the core level of the vertex to. If attr is provided, the core level of the vertex will be saved to this attribute of the vertex.

STRING file_path

If file_path is provided, the algorithm will output results to a file specified by the file path in CSV format.

BOOL print_all_k

Whether to print all k connections

BOOL show_shells

The k-shell is the set of vertices that are part of the k-core but not part of the (k+1)-core. If show_shells is true, the algorithm will return the k-shells found for every value of k. within the range provided. For each k-shell, the results will include its member vertices.

Time complexity

\$O(E)\$, where \$E\$ is the number of edges in the graph.

Run commands

Schema-Free Query

RUN QUERY tg_kcore (<parameters>)

Packaged Template Query

CALL GDBMS_ALGO.community.kcore (<parameters>)

Example

In the example below based on the social graph from GSQL 101, we can see that Dan, Tom, and Jenny make up a 2-core, which is the max-core of the graph:

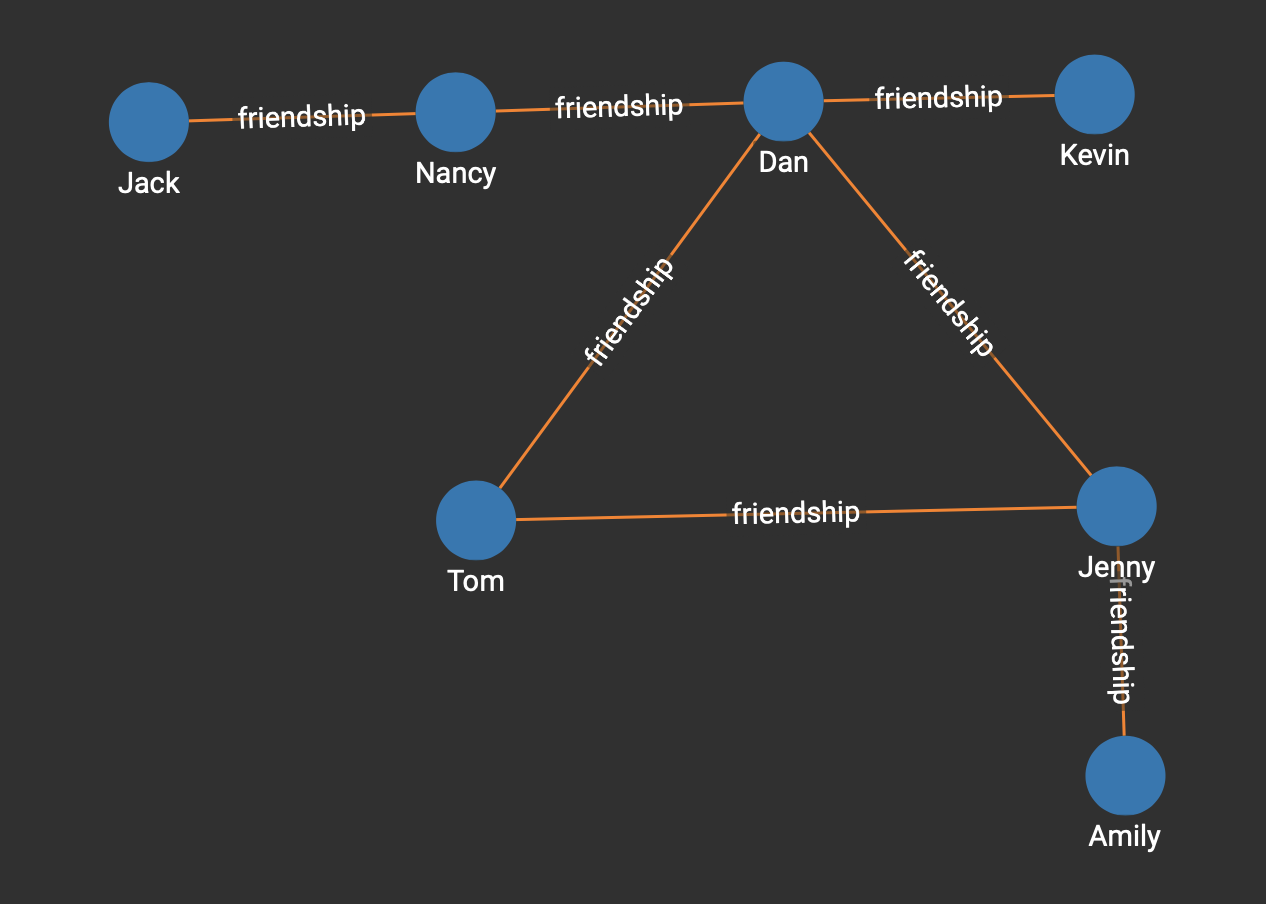
image

If we run the kcore algorithm on this small graph like so:

RUN QUERY tg_kcore("person", "friendship", 0, -1, TRUE, "", "", FALSE, FALSE)

Here is the returned JSON response, which includes a 2-core that is comprised of Dan, Jenny, and Tom:

[
  {
    "core_size": 3,
    "k": 2,             // the k-core with the highest possible k is returned
    "max_core": [
      {
        "attributes": {
          "@core": 2,
          "@deg": 0,
          "age": 40,
          "gender": "male",
          "name": "Tom",
          "state": "ca"
        },
        "v_id": "Tom",
        "v_type": "person"
      },
      {
        "attributes": {
          "@core": 2,
          "@deg": 0,
          "age": 34,
          "gender": "male",
          "name": "Dan",
          "state": "ny"
        },
        "v_id": "Dan",
        "v_type": "person"
      },
      {
        "attributes": {
          "@core": 2,
          "@deg": 0,
          "age": 25,
          "gender": "female",
          "name": "Jenny",
          "state": "tx"
        },
        "v_id": "Jenny",
        "v_type": "person"
      }
    ]
  }
]