Weisfeiler-Lehman Isomorphism

Supported Graph Characteristics

Unweighted edges

Directed edges

Undirected edges

Homogeneous vertex types

Algorithm link: Weisfeiler-Lehman

This algorithm identifies isomorphic subgraphs in a graph, and labels the corresponding vertices isomorphic graphs.

Two graphs are considered isomorphic if there is a mapping between the nodes of the graphs that preserves node adjacencies. That is, a pair of nodes may be connected by an edge in the first graph if and only if the corresponding pair of nodes in the second graph is also connected by an edge in the same way. An example of two isomorphic graphs is shown here[1]:

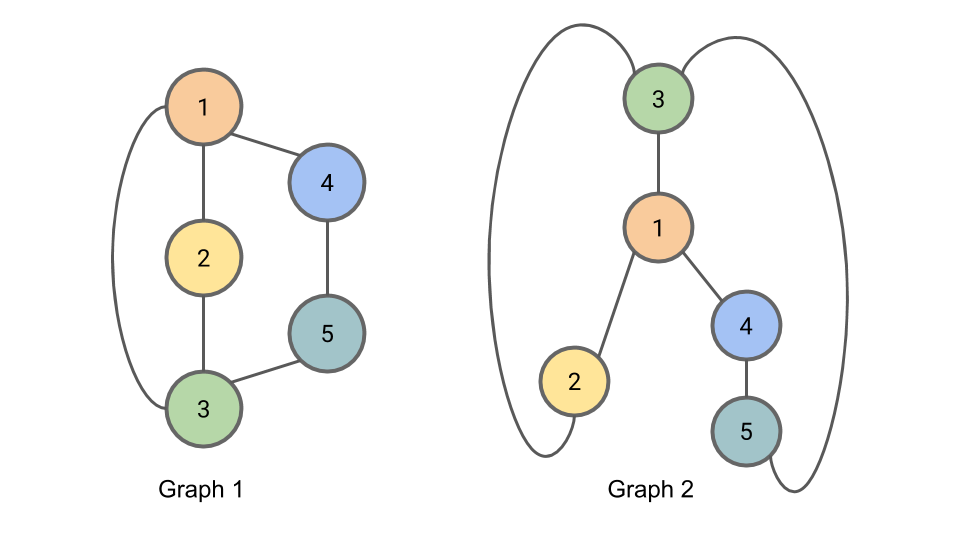
graph isomorphism
Figure 1. Graph 1 and Graph 2 are isomorphic. The correspondence between nodes is illustrated by the node colors and numbers.

This algorithm gives every vertex in the graph a label. It finds the isomorphic subgraphs, and gives every vertex in the isomorphic subgraphs the same label.

Specifications

CREATE QUERY tg_weisfeiler_lehman(STRING v_type,STRING e_type,
    INT depth, INT out_put_limit, BOOL print_results = TRUE,
    STRING result_attribute = "",STRING file_path = "")

Parameters

Parameter Descriptiono

STRING v_type

Vertex type to consider.

STRING e_type

Edge type to traverse.

INT depth

Number of hops to consider

INT out_put_limit

If print_results is set to true, print a maximum of this number of vertices..

BOOL print_results

If true, print JSON to standard output.

STRING result_attribute

If not empty, save the label of each vertex to this attribute.

STRING file_path

If not empty, save the result in CSV format to this filepath.

Output

When print_results is set to true, the @current_label accumulator on a vertex represents the final label of the vertex. If two vertices share a label, it means that they are corresponding vertices in two isomorphic subgraphs.

Time complexity

This algorithm has a time complexity of \$O(V*E)\$, where \$V\$ is the number of vertices and \$E\$ is the number of edges.

Space complexity

This algorithm has a time complexity of \$O(V)\$, where \$V\$ is the number of vertices.

Run commands

Schema-Free Query

RUN QUERY tg_weisfeiler_lehman (<parameters>)

Packaged Template Query

CALL GDBMS_ALGO.graphML.weisfeiler_lehman (<parameters>)

Example

Suppose we have the following graph:

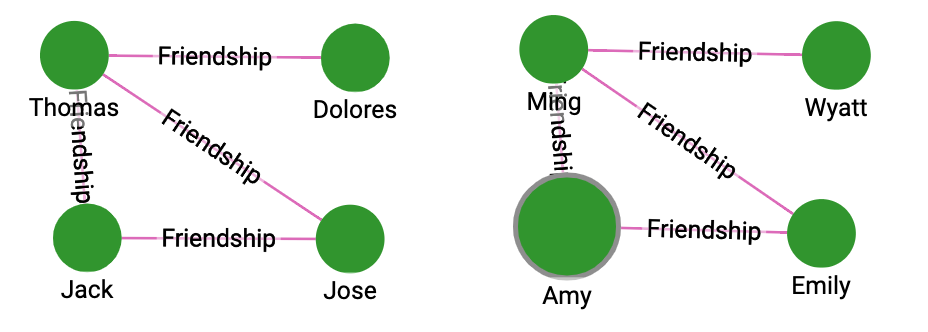
weisfeiler lehman ex

We can see that there are two distinct subgraphs that are isomorphic. Running the algorithm on the graph produces the following results：

  • Query

  • Results

RUN QUERY tg_weisfeiler_lehman ("Person", "Friendship", 3, 8, true, _, _)

We can see in the results that corresponding vertex pairs such as Emily and Jose share the same label.

[
  {
    "Start": [
      {
        "attributes": {
          "@current_label": "237612459038074888",
          "@label_list": [],
          "@previous_label": "1"
        },
        "v_id": "Wyatt",
        "v_type": "Person"
      },
      {
        "attributes": {
          "@current_label": "13342665574248803982",
          "@label_list": [],
          "@previous_label": "1"
        },
        "v_id": "Emily",
        "v_type": "Person"
      },
      {
        "attributes": {
          "@current_label": "13342665574248803982",
          "@label_list": [],
          "@previous_label": "1"
        },
        "v_id": "Jose",
        "v_type": "Person"
      },
      {
        "attributes": {
          "@current_label": "6556095808804302272",
          "@label_list": [],
          "@previous_label": "1"
        },
        "v_id": "Thomas",
        "v_type": "Person"
      },
      {
        "attributes": {
          "@current_label": "13342665574248803982",
          "@label_list": [],
          "@previous_label": "1"
        },
        "v_id": "Amy",
        "v_type": "Person"
      },
      {
        "attributes": {
          "@current_label": "237612459038074888",
          "@label_list": [],
          "@previous_label": "1"
        },
        "v_id": "Dolores",
        "v_type": "Person"
      },
      {
        "attributes": {
          "@current_label": "13342665574248803982",
          "@label_list": [],
          "@previous_label": "1"
        },
        "v_id": "Jack",
        "v_type": "Person"
      },
      {
        "attributes": {
          "@current_label": "6556095808804302272",
          "@label_list": [],
          "@previous_label": "1"
        },
        "v_id": "Ming",
        "v_type": "Person"
      }
    ]
  }
]
1. David Bieber, The Weisfeiler-Lehman Isomorphism Test, https://davidbieber.com/post/2019-05-10-weisfeiler-lehman-isomorphism-test/