Eigenvector Centrality

Supported Graph Characteristics

Unweighted edges

Directed edges

Undirected edges

Homogeneous vertex types

Heterogeneous vertex types

Eigenvector centrality (also called eigencentrality or prestige score) is a measure of the influence of a vertex in a network. Relative scores are assigned to all vertices in the network based on the concept that connections to high-scoring vertices contribute more to the score of the vertex in question than equal connections to low-scoring vertices.

A high eigenvector score means that a vertex is connected to many vertices who themselves have high scores.

Specifications

CREATE QUERY tg_eigenvector_cent(SET<STRING> v_type_set, SET<STRING> e_type_set,
 INT maximum_iteration = 100, FLOAT conv_limit = 0.000001, INT top_k = 100,
 BOOL print_results = True, STRING result_attribute = "", STRING file_path = ""
 )

Parameters

Name Description Default value

Name	Description	Default value
`SET<STRING> v_type_set`	Vertex types to assign scores to.	(empty set of strings)
`SET<STRING> e_type_set`	Edge types to traverse.	(empty set of strings)
`INT maximum_iteration`	Maximum number of iteration.	100
`FLOAT conv_limit`	The convergence limit.	0.000001
`INT top_k`	The number of vertices with the highest scores to return.	100
`BOOL print_results`	If true, print results to JSON output.	True
`STRING result_attribute`	If not empty, save the score of each vertex to this attribute.	(empty string)
`STRING file_path`	If not empty, print results in CSV to this file.	(empty string)

SET<STRING> v_type_set

Vertex types to assign scores to.

(empty set of strings)

SET<STRING> e_type_set

Edge types to traverse.

(empty set of strings)

INT maximum_iteration

Maximum number of iteration.

100

FLOAT conv_limit

The convergence limit.

0.000001

INT top_k

The number of vertices with the highest scores to return.

100

BOOL print_results

If true, print results to JSON output.

True

STRING result_attribute

If not empty, save the score of each vertex to this attribute.

(empty string)

STRING file_path

If not empty, print results in CSV to this file.

(empty string)

Output

Returns an eigenvector centrality score for all vertices of the specified type in the graph. The results are ordered from most central to least central.

There is an optional parameter, top_k, that limits the results to an arbitrary number of vertices with the highest scores in the graph. This can be useful for larger graphs, since in large graphs there are likely to be many vertices with very low centrality.

The maximum result size is equal to \(V\), the number of vertices, because one centrality score is calculated for each vertex.

Time complexity

The algorithm has a time complexity of \(O(E*k)\), where \(E\) is the number of edges and \(k\) is the number of iterations.

The number of iterations is data-dependent, but the user can set a maximum. Parallel processing reduces the time needed for computation.

Example

Suppose we have the following graph:

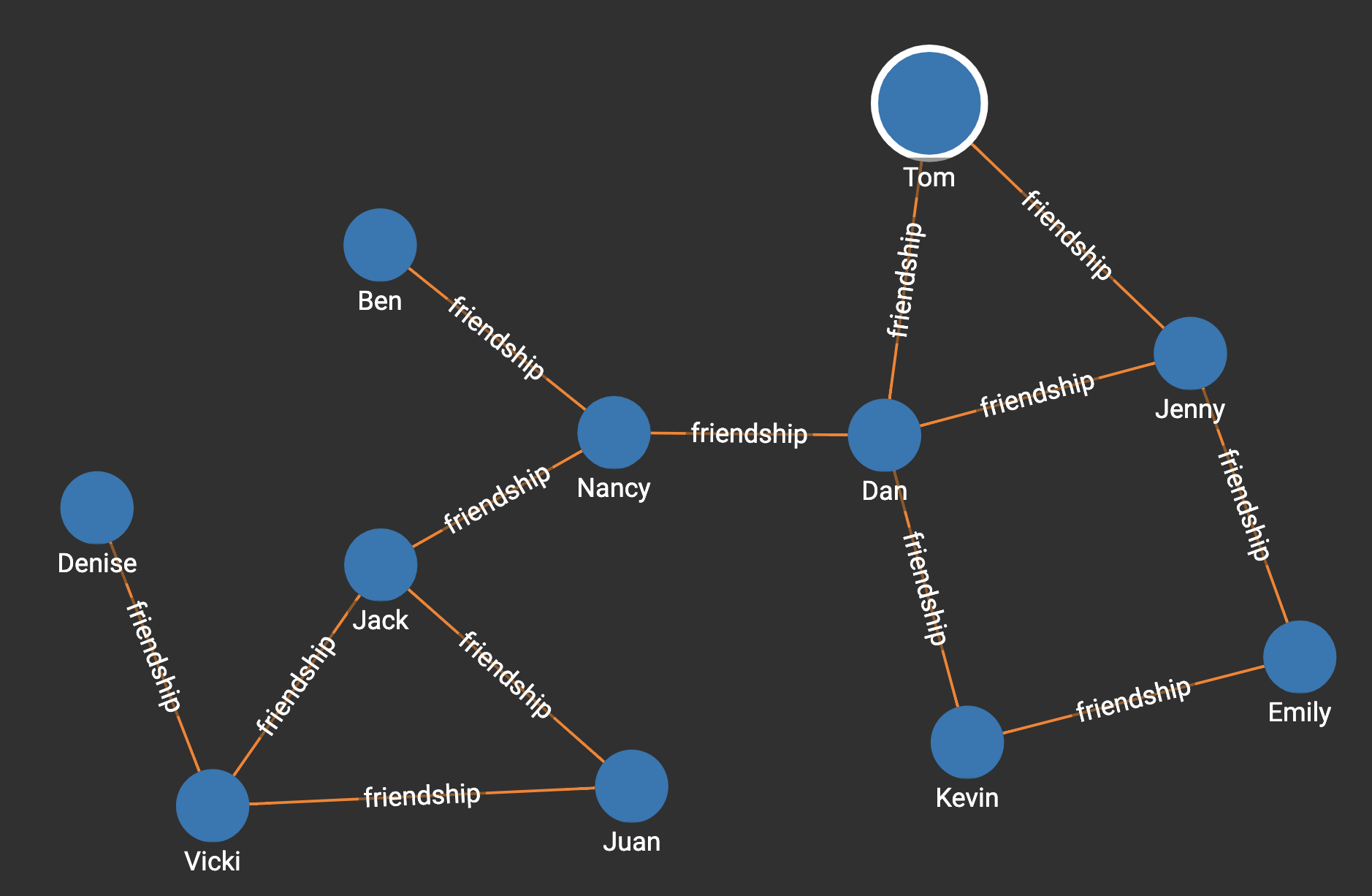
Running the algorithm on the graph will show that Dan has the highest centrality score.

Query
Result

RUN QUERY tg_eigenvector_cent(["person"], ["friendship"])

[
  {
    "top_scores": [
      {
        "Vertex_ID": "Dan",
        "score": 0.52728
      },
      {
        "Vertex_ID": "Jenny",
        "score": 0.42913
      },
      {
        "Vertex_ID": "Tom",
        "score": 0.35588
      },
      {
        "Vertex_ID": "Nancy",
        "score": 0.33529
      },
      {
        "Vertex_ID": "Kevin",
        "score": 0.2967
      },
      {
        "Vertex_ID": "Emily",
        "score": 0.27009
      },
      {
        "Vertex_ID": "Jack",
        "score": 0.24902
      },
      {
        "Vertex_ID": "Vicki",
        "score": 0.17584
      },
      {
        "Vertex_ID": "Juan",
        "score": 0.15809
      },
      {
        "Vertex_ID": "Ben",
        "score": 0.12476
      },
      {
        "Vertex_ID": "Denise",
        "score": 0.06543
      }
    ]
  }
]